前向&反向传播&链式法则
神经网络
通俗理解,神经网络就是给一组输入,经过神经网络的运算后,得到一个在误差范围内的结果。模型的选择和对模型中各个神经元的系数的确定决定了模型的输出结果,为了得到期望的结果,需要有多组输入,和对应的正确结果,用这些数据来训练模型,确定合适的参数组合。参数确定后,即可预测新的输入对应的输出。
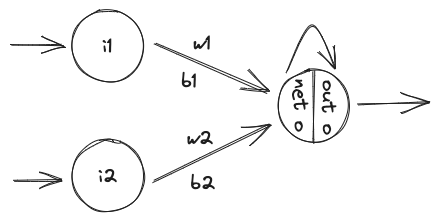
举一个简单的例子,两个神经元组成一个一层的神经网络,给定的两个输入,能够得到一个结果。
前向传播
通俗理解前向传播,就是根据输入计算输出的过程。按上述例子来说,就是 \[ net_o = i1×w1+b1 + i2×w2+b2 \] 假定输入数据为:
1 | i1 = 0.05, i2 = 0.10; |
那么: \[ net_o = i1×w1+b1 + i2×w2+b2 = 0.05×0.15+0.35+0.10*0.20+0.60=0.9775 \] 假定选择sigmoid函数作为激活函数,那么 \[ out_o = \frac{1}{1+\epsilon^{net_o}}=\frac{1}{1+\epsilon^{0.9775}}=0.2734 \]
如果此时我们期望的输出为:
1 | o=0.01 |
误差为 \[ o-out_o=0.01-0.2734=-0.2634 \]
梯度下降法
考虑一个抛物线函数: \[ y=f(x)^2 \]
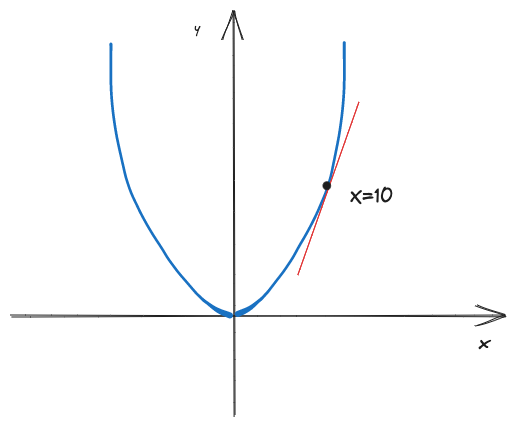
X轴为权值,Y轴为误差,那么我们能计算得到曲线斜率为0的位置为最低位置(x=0),如果是一个复杂的多维函数,不容易直接通过计算得出曲线或者平面的最低位置,所以可以使用梯度下降法来通过迭代计算最低位置。相当于放一个小球,小球会在重力的影响下,沿最陡的方向下降。
假设目前在x=10的点上(x0),梯度为: \[ \nabla f(x_0)=f'(x0)=2x=20 \] 那梯度的反方向就是下降率最快的方向,如果步长为η=0.2,那么新的位置x1为: \[ x_1 = x_0 - \eta×\nabla f(x_0)=10-0.2*20=6 \] 然后继续迭代,直到梯度曲线趋近于0.
| x0 | x1 | x2 | x3 | x4 | x5 | x6 | X7 | x8 | x9 | X10 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 梯度 | 20 | 12 | 7,2 | 4.32 | 2.59 | 1.56 | 0.93 | 0.56 | 0.34 | 0.2 | 0.12 |
注意步长的选择,如果步长太小,那么经过多次迭代仍然无法达到曲线或者平面的最低点,如果步长过长,那么或跳过最低点,从而不收敛。
同理,可以从二维(一元函数,曲线)推广到三维(二元函数,平面)甚至多维,目标就是找到最陡的反向,然后按步长走到下一个位置,然后一直迭代下去。
反向传播
假设使用均方误差(MSE)来作为误差评估方法,那么误差为(这个是MSE么???): \[ E=\Sigma\frac{1}{2}(o-out_o)^2 \] 由于这个例子中只有一个输出,那么误差为: \[ E=\frac{1}{2}(0.01-0.2734)^2=0.03468978 \] 反向传播就是通过误差来计算当前参数的梯度,然后沿梯度下降的方向走一个步长η,迭代此过程。
根据正向传播的函数,能够得到: \[ out_o = \frac{1}{1+\epsilon^{net_o}} = \frac{1}{1+\epsilon^{(i1×w1+b1 + i2×w2+b2)}} \]
\[ E=\Sigma\frac{1}{2}(o-out_o)^2=\Sigma\frac{1}{2}(o-\frac{1}{1+\epsilon^{(i1×w1+b1 + i2×w2+b2)}})^2 \]
我们要计算梯度,也就是要计算总的误差E在w1和w2的偏导值。
这个公式比较复杂,所以要使用到求导的链式法则。
链式法则
\[ \frac{\partial E}{\partial w1}=\frac{\partial E}{\partial out_o}×\frac{\partial out_o}{\partial net_o}×\frac{\partial net_o}{\partial w1} \]
那么,上述复杂函数的求导就可以转换成几个简单函数求导的乘积。 \[ \frac{\partial E}{\partial out_0}=2×\frac{1}{2}(o-out_o)^1*-1+0=(0.01-0.2734)*-1=0.2634 \]
\[ \frac{\partial out_o}{\partial net_o}=out_o(1-out_o)=0.2734(1-0.2734)=0.19865244 \]
\[ \frac{\partial net_o}{\partial w1}=i1=0.05 \]
相乘可得: \[ \frac{\partial E}{\partial w1}=0.2634×0.19865244×0.05=0.0002616 \] 同理: \[ \frac{\partial E}{\partial w2}=0.2634×0.19865244×0.10=0.0052325 \] 如果步长η=0.2,那么: \[ w1' = w1 - \eta×\frac{\partial E}{\partial w1} =0.004994768 \]
\[ w2' = w2 - \eta×\frac{\partial E}{\partial w2} =0.0989535 \]
然后,使用更新后的权值做下一步迭代。